Für den Mathematikunterricht gibt es verschiedene Prinzipien, also eine Art Strukturierungshilfe für den Aufbau von Sequenzen, mit dem Ziel einen möglichst großen Lerneffekt bei den Kindern zu erreichen. In meiner Ausbildung wurde vor allem Wert auf das E-I-S-Prinzip nach dem amerikanischen Kognitions- und Entwicklungspsychologen Jérôme Bruner gelegt, bei dem ein Lerngegenstand auf unterschiedlichen Darstellungsebenen durchdrungen werden soll.
Wofür steht die Abkürzung E-I-S?
Das „E“ steht für enaktiv, also eine aktiv handelnde Auseinandersetzung mit dem Lerngegenstand. Die zweite Ebene ist die ikonische, die mit dem „I“ abgekürzt wird. Dabei geht es um die bildliche Darstellung einer mathematischen Operation. Und die letzte Ebene ist schließlich die symbolische, für die das „S“ steht. Hiervon spricht man, wenn eine Rechenaufgabe z.B. mündlich formuliert oder schriftlich notiert wird.
Ein Beispiel aus der Praxis
Um das Ganze ein wenig zu verdeutlichen, kommt nun ein praktisches Beispiel aus meinem Unterricht. In einem meiner letzten Beiträge habe ich davon berichtet, wie ich mit meinen ZweitklässlerInnen ein Einmaleinsbuch mit der App „Book Creator“ erstellt habe. Dabei sollten die Kinder im Klassenzimmer Einmaleinsaufgaben finden und mit dem Tablet fotografieren.
Übertragen auf das E-I-S-Prinzip bedeutet das: Auf der enaktiven Ebene haben die Kinder hier also z.B. mithilfe von Stiften eine Einmaleinsaufgabe gelegt und ausgerechnet.

Im ikonischen Modus werden Bilder als Lerngegenstand verwendet. Die Fotos, die die Kinder von ihren Aufgaben geschossen haben, repräsentieren also Einmaleinsaufgaben auf der ikonischen Ebene. Dazu zählen aber z.B. auch Bilder, die im Mathebuch oder auf Arbeitsblättern zu sehen sind und die eine Aufgabe darstellen.
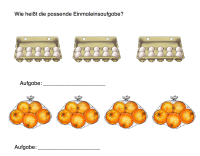
Die letzte Darstellungsebene kommt schließlich ohne jegliches Anschauungsmaterial aus und es wird auf einer abstrakten sprachlichen oder numerischen Ebene gearbeitet. Das heißt, die die mathematischen Operationen werden entweder nur sprachlich formuliert oder als Aufgabe aufgeschrieben und schließlich ausgerechnet.

Das E-I-S-Prinzip als Strukturierungshilfe für eine Sequenz
Bruners Empfehlung ist nun, einen mathematischen Sachverhalt möglichst immer in allen drei Darstellungsebenen zu behandeln, um bei den Kindern ein tieferes Verständnis von den mathematischen Operationen zu erreichen. Dabei ist es sinnvoll, in dieser Reihenfolge, also von der enaktiven über die ikonische zur symbolischen Darstellungsebene, vorzugehen. Doch auch ein gezielter und bewusster Wechsel zwischen den Ebenen vertieft die gedankliche Durchdringung des Lerngegenstands. Bei den Einmaleinsaufgaben heißt das z.B., dass die Kinder zu der Aufgabe 5x6 ein passendes Bild malen.
Ziel ist letztendlich, dass die SchülerInnen im Laufe einer Sequenz beim Rechnen immer weniger auf konkretes Material oder Bilder angewiesen sind und mentale Vorstellungen entwickeln, die sie flexibel auch auf neue Aufgaben und Situationen anwenden können. Damit ist das E-I-S-Prinzip auch ein gutes Hilfsmittel, wenn man feststellt, dass Kinder noch Probleme bei bestimmten Aufgaben haben: Indem man immer wieder zwischen den Darstellungsebenen wechselt und schwächeren Kindern Material zur handelnden Auseinandersetzung mit den verschiedenen Aufgaben anbietet, werden diese mentalen Vorstellungen von Rechenaufgaben gefördert. So macht es hoffentlich irgendwann „Klick“ und sie haben verstanden, wie Einmaleinsaufgaben funktionieren. Und der Rest ist dann eine Übungssache.